kapitel-03maple.mw
Mathematik
von T. Arens, F. Hettlich, Ch. Karpfinger, U. Kockelkorn, K. Lichtenegger, H. Stachel
(zu Kapitel 3: Rechentechniken)
Termumformungen
Eine nuetzliche Eigenschaft von CAS Systemen ist die formale Umformung von algebraischen Ausdruecken.
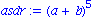
Eine Vielzahl von Befehlen, um solche Ausdruecke umzuformen, auszumultiplizieren oder zu kombinieren steht zur Verfuegung. So liefert zum Beispiel der Befehl
expand
eine ausmultiplizierte Version eines Ausdrucks.

Oder retour mit dem Befehl
factor
, der ein gegebenes Polynom versucht zu faktorisieren:
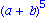
Hier haben wir das Ditto Zeichen
%
in Maple genutzt, dass schlicht das vorhergegangene Resultat bezeichnet. Auch Gleichungen und Ungleichungen lassen sich behandeln. Der Befehl
simplify
"vereinfacht" Ausdruecke stufenweise.
| > |
asdr:= asdr- a^5-10*a^2*b^3 - 5*a*b*(a^3+b^3);
simplify(asdr); |
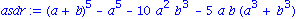
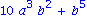
Sind zur Vereinfachung eines Ausdrucks Eigenschaften bestimmter Funktionenklassen erforderlich, so muessen diese durch eine zusaetzliche Option angeben werden. Wollen wir etwa Additionstheoreme bei trogonometrischen Ausdruecken nutzen, so ist die Option
trig
erforderlich.
| > |
r := ( sin(x)^2 + cos(2*x) ) / cos(x)^2 ;
simplify(r,trig); |
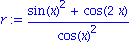

Gleichungen
Einer der maechtigsten Befehle in Maple ist der Befehl
solve
, um Gleichungen nach einer Variablen aufzuloesen. Wir koennen diesen Befehl nutzen, um etwa quadratische Gleichungen zu loesen. Geben wir zunaechst eine Gleichung ein
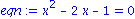
Die beiden Loesungen dieser Gleichung erhalten wir durch
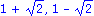
Beachten Sie, dass das erste Argument in diesem Befehl die zu loesende Gleichung beinhaltet und das zweite Argument die Variable angibt, nach der die Gleichung aufgeloest werden soll. Im allgemeinen wird von komplexwertigen Variablen ausgegangen, so dass zwei der drei Loesungen bei
| > |
solve( x^3-x^2-x-2=0, x ); |
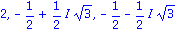
eine Form haben, die Sie erst verstehen koennen, wenn Sie die komplexen Zahlen kennengelernt haben.
Auch andere Gleichungen lassen sich mit Hilfe dieses Befehls loesen. So ergibt etwa
| > |
solve( sin(x)+cos(x)=sqrt(2), x ); |
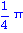
Wegen der Periodizitaet der trigonometrischen Ausdruecke gibt es offensichtlich weitere Loesungen neben der angezeigten. Um alle Loesungen (die Maple findet) angezeigt zu bekommen muss eine globale Variable umgesetzt werden.
| > |
_EnvAllSolutions := true:
solve( sin(x)+cos(x)=sqrt(2), x ); |
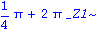
Die Hilfsvariable 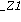 wurde zur Ausgabe aller Loesungen vom System eingefuehrt. Das Symbol ~ an einer Variablen kennzeichnet, dass Bedingungen an diese Variable geknuepft sind. Mit
wurde zur Ausgabe aller Loesungen vom System eingefuehrt. Das Symbol ~ an einer Variablen kennzeichnet, dass Bedingungen an diese Variable geknuepft sind. Mit
Originally _Z1, renamed _Z1~:
is assumed to be: integer
bekommen wir die Information, dass _Z1 eine beliebige ganze Zahl ist.
Summen
Der Befehl
sum
summiert eine angebene Liste von Zahlen. Im ersten Argument ist der Ausdruck anzugeben, der summiert werden soll. Das zweite Argument beschreibt den Laufindex und die Summationsgrenzen.
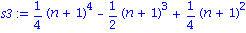
Mit
sub
laesst sich nun der Parameter n im Ausdruck s3 durch eine Zahl ersetzen ("substitute").
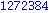
Die Terme im ersten Argument des Befehls sum werden algebraisch ausgewertet. Wenn dies nicht moeglich ist , wird der Ausdruck mit Hilfe des Summenzeichens angegeben. Zum Beispiel ein allgemeines Polynom vom Grad n mit Koeffizienten ![a[j]](images/kapitel-03maple_16.gif) .
.
| > |
sum(a[j]*x^j,j=0..n+1); |
![sum(a[j]*x^j, j = 0 .. n+1)](images/kapitel-03maple_17.gif)
Selbstverstaendlich sind auch die Fakultaet, der Binomialkoeffizient und das Produktzeichen in Maple bekannt.
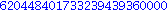
![product(a[j], j = 1 .. n)](images/kapitel-03maple_21.gif)
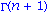
Zur Beschreibung des letzten Resultats wird nicht das ! genutzt sondern die allgemeinere
Gamma Funktion
. Das Ergebnis bleibt selbstverstaendlich gleich (testen Sie wieder n=24 beim letzten Befehl).
Aufgaben
(Um Aufgaben zu bearbeiten oeffnen Sie bitte ein neues Worksheet und probieren Sie dort ihre Befehle aus. Einen Loesungsvorschlag erhalten Sie, wenn sie die Loesung oeffnen. Dies sollten Sie aber erst nach eigenen Versuchen nutzen.)
1. Gegeben sind die Polynome p := 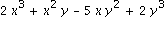 und q :=
und q := 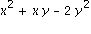 . Faktorisieren Sie diese Polynome und finden Sie eine einfache Darstellung der rationalen Funktion p/q.
. Faktorisieren Sie diese Polynome und finden Sie eine einfache Darstellung der rationalen Funktion p/q.
Loesung
2. Bestimmen Sie Formeln fuer die Summen 1+2+3+ . . . +n und  +
+ + . . . +
+ . . . + und geben Sie die Werte fuer
und geben Sie die Werte fuer  an.
an.
Loesung
3. Berechnen Sie
 ,
,  ,
,  ,
, 
Loesung
4. Finden Sie eine Loesung der Gleichung 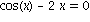
Loesung
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 ,
,  ,
,