Intgralrechnung

Die Stammfunktion zu einem gegebenen Ausdruck wird in Maple durch den Befehl int bestimmt.

>	int(x*ln(x),x);

Wenn fuer die Integrationsvariable ein Bereich angegeben wird, so wird das bestimmte Integral ausgewertet.

>	int(ln(x)/sqrt(x),x=0..1);

Offensichtlich werden auch unbeschraenkte Funktionen und/oder Intervalle  beruecksichtig. Wir koennen zum Beispiel  auch die Laplacetransformierte zu bestimmen.

>	assume(s>0); int(t*exp(-s*t),t=0..infinity);

Dabei ist aber die Voraussetzung an erforderlich, damit die Existenz des Integrals gesichert ist.

Eine ganze Reihe von Integralen, die nicht geschlossen auswertbar sind, sind als Funktionen bekannt. So erhalten wir  

>	int(sin(x)/x,x); int(exp(-x^2),x);

( erf, ... ). Geben wir Intervallgrenzen in solchen Faellen an, so wird als Resultat der entsprechende Ausdruck angezeigt.

>	int(sin(x)/sqrt(x),x=0..1);

Eine numerische Auswertung erreichen wir durch

>	evalf(int(sin(x)/sqrt(x),x=0..1));

(siehe int[numerical] ). Eine numerische Berechnung eines Integrals ohne die vorhergehende algebraische Behandlung, laesst sich auch erzwingen. Dazu dient der Befehl Int , der zunaechst keine Auswertung des Inetgrals durchfuehrt. Zusammen mit evalf wird ein numerisches Verfahren zur Approximation des bestimmten Integrals herangezogen.

>	Int(sqrt(x)/sin(x),x=0..1); evalf(%);

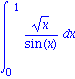
Wenn nichts anderes vereinbart ist, wird das Clenshaw-Curtis Verfahren zum numerischen Integrieren verwandt. Es lassen sich auch andere Verfahren (z.B. eine Newton-Cotes Formel) auswaehlen. Ausserdem kann  die Anzahl der genauen Dezimalstellen (hier 20) festgelegt werden.

>	evalf(Int((x^3+1)/(x^5-x^2+1),x=0..1, 20, _NCrule));

Im Paket "student" sind unter anderem auch die Trapez- und die Simpsonregel zu finden.

>	with(student);

(Bem.: Leider ist der  Befehle Int jetzt leicht modifiziert, so dass die numerischen Optionen wie oben beschrieben nicht mehr akzeptiert werden. Sie koennen dies mit restart wieder rueckgaengig machen).

>	trapezoid(x^n*sin(x),x=0..Pi); simpson(x^n*sin(x),x=0..Pi);

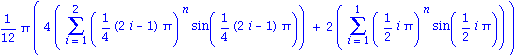
Die Anzahl der Stuetzstellen laesst sich  durch ein zusaetzliches Argument frei waehlen.

>	simpson(x^3*sin(x),x=0..Pi,20); evalf(%);

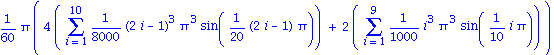
Mit einer Schleife koennen wir  nun leicht eine Tabellen erzeugen, um das Konvergenzverhalten zu studieren,

>	a:=evalf(1/4*(1-exp(-4))): for j from 2 to 6 do   2^j, abs(evalf(trapezoid(exp(-4*x),x=0..1,2^j))-a),     abs(evalf(simpson(exp(-4*x),x=0..1,2^j))-a); od;

In Hinblick auf die Partialbruchzerlegung, ist es nuetzlich an dieser Stelle auf einige Umformungen rationaler Ausdrueck einzugehen. Betrachten wir zum Beispiel den Ausdruck

>	r:=(x^3+2*x^2-x+1)/(x^3-2*x^2-x+2);

Die Partialbruchzerlegung von erhalten wir durch convert mit entsprechender Option.

>	convert(r,parfrac,x);

Um einzelne Schritte zu ueberpruefen, definieren wir zunaechst mit den Befehlen numer und denom  Zaehler- und Nennerpolynom.

>	p:=numer(r); q:=denom(r);

Eine Polynomdivision ist durch

>	r1:=quo(p,q,x) + rem(p,q,x)/q;

gegeben, d.h. quo ermittelt den Quotienten und rem den  Rest. Wir pruefen das Resultat durch

>	evalb(r=normal(r1));

Neben dem Befehl normal sind auch weitere Umformungsbefehle nuetzlich, z.B.

>	expand(r);

(siehe weitere Hinweise in den Hilfen). Die Faktorisierung des Nenners ergibt sich aus

>	factor(q);

>

Aufgaben

(Um Aufgaben zu bearbeiten oeffnen Sie bitte ein neues Worksheet und probieren Sie dort ihre Befehle aus. Einen Loesungsvorschlag erhalten Sie, wenn sie die Loesung oeffnen. Dies sollten Sie aber erst nach eigenen Versuchen nutzen.)

1. Berechnen Sie die bestimmten Integrale
     ,         ,          

>

2. Bestimmen Sie Stammfunktionen zu folgenden Funktionen,

        a)    f(x) = ,                                   b)    f(x) =   ,
  

       c)    f(x) = ,                     d)    f(x) = .  

>

3.  Fuehren Sie eine Polynomdivision von  

  und  

    durch und bestimmen Sie die Partialbruchzerlegung von p/q.

>

>