Weitere Befehle zum Umgang mit Matrizen finden sich indem Paket linalg. Wie wir im Programm des letzten Abschnitt schon gesehen haben, koennen wir mit coldim oder rowdim  die Spalten-  bzw.  Zeilendimension einer Matrix erfragen. Mit transpose laesst sich die transponierte Matrix angeben.

>	with(linalg): transpose(A);

Warning, the protected names norm and trace have been redefined and unprotected

oder komplexwertig

>	A:=array([[1+I, 1+I], [1,1-I] ]); transpose(A); htranspose(A);

Mit dem Befehl htranspose erhalten Sie die transponierte konjugiert komplexe Matrix, die man  als hermitsch transponierte Matrix bezeichnet.

Mit einigen Befehlen lassen sich Matrizen mit einer speziellen Gestalt leichter eingeben. So erhalten wir etwa eine Diagonalmatrix durch

>	diag(2,3,4,5);

Eine Einheitsmatrix bekommen wir somit durch

>	diag(1,1,1);

Eine Matrix, die auf den Diagonalen gleiche Eintraege hat, heisst Toeplitzmatrix . Eine symmetrische Toeplitzmatrix ergibt sich zum Beispiel  durch

>	toeplitz([1,2,3,4]);

Die Vielzahl von Befehle etwa zu

symmetrische Matrizen oder Bandmatrizen.  Die Vielzahl von Befehlen zum Umgang mit Matrizen/Feldern wollen wir hier nicht alle aufzaehlen, aber es lohnt sich die Befehlsliste zum Paket linalg genauer durchzusehen.

>

Wenn eine inverse Matrix existiert, berechnet der Befehl  inverse  diese Inverse.

>	A:= matrix(4,4,[[1,2,3,4],[1,1,0,0],[0,2,1,0],[2,5,1,4]]);   inverse(A);

Leicht laesst sich pruefen, ob eine Matrix orthogonal ist. Betrachten wir etwa eine der Matrizen aus der Selbstfrage auf Seite 534  

>	B:=matrix(3,3,[[0,-1,0],[0,0,-1],[-1,0,0]]); evalm(transpose(B)&*B);

Also ist die Matrix orthogonal, die transponierte Matrix ist gerade die Inverse zu A.

>	inverse(B); transpose(B);

Die LR-Zerlegung einer Matrix ist durch den Befehl, LUdecomp, im Paket linalg vertreten. Der Befehl liefert als Ergebnis die Matrix U, die  obere  Dreiecksmatrix. (Im Englischen werden die beiden Matrizen mit  U fuer  upper und  L fuer  lower bezeichnet anstelle von L fuer linke unterer Dreiecksmatrix und R fuer rechte obere Dreiecksmatrix bezeichnet)  

>	LUdecomp(A,L='l',U='u',P='p');

Mit den zusaetzlichen Argumenten hat der Befehl die Variablen l,u,p mit den entsprechenden Matrizen belegt, sodass die Identitaet 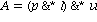gilt, wie wir schnell nachpruefen.

>	evalm(l); evalm(u); evalm(p); evalm(A) = evalm(p&*l&*u);

Beachten Sie, dass die von Maple gelieferte Vertauschungsmatrix p gerade die Inverse der im Buch angegebenen Matrix P  (s. Seite 537) ist.

Ob eine Matrix ueberhaupt invertierbar ist, koennen wir  leicht anhand der Determinate pruefen, die mit dem Befehl det berechnet wird.

>

det(A);

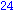
Die Adjunkte einer Matrix A bekommt man  direkt  durch

>	adjoint(A);

Wir koennen diese Matrix natuerlich auch durch multiplizieren der Inverse von A mit det(A) berechnen.

>	evalm(det(A)*inverse(A));

>

Loesung

Loesung

Loesung