kapitel-04maple.mw
Mathematik
von T. Arens, F. Hettlich, Ch. Karpfinger, U. Kockelkorn, K. Lichtenegger, H. Stachel
(zu Kapitel 4: Elementare Funktionen)
Ausdruecke / Funktionen
In einem Compueralgebrasystem wie Maple muss sauber unterschieden werden zwischen einer Funktion und einem Ausdruck. Daher gibt es zwei Moeglichkeiten Funktionen anzugeben. Es ist also wichtig, wie es auch im Buch ausfuehrlich diskutiert wird, zwischen Funktionen und Ausdruecken zu unterscheiden.
1. als Operator (Operation, Prozedur, Funktion):
| > |
f:=x-> cos(exp(-x^2));
f(2);
evalf(f(2)); |
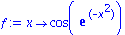
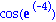
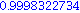
Bei der Darstellung als Operator ist "f" eine Prozedur (
proc
). Wie gezeigt, kann durch Aufrufen mit einem Argument die Funktion ausgewertet werden (mit
evalf
in Gleitkommaarithmetik).
2. als algebraischer Ausdruck (
expression
)
| > |
a:=cos(exp(-x^2));
subs(x=2,a);
evalf(%); |
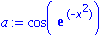
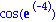
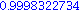
Das Kommando a(2) ist hier nicht sinnvoll. Aber mit dem Befehl
subs
laesst sich der Ausdruck "x" in a ersetzen, sodass der neue Ausdruck dann etwa als Gleitkommazahl auswertbar ist.
Durch
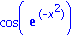
wird der Ausdruck zum Operator f mit der Variablen x erzeugt. Und durch den Befehl
unapply
wird der oben definierte Ausdruck a in einen Operator konvertiert.
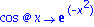
(Das Symbol "@" (
atsign
) bedeutet die Verkettung der beiden Operatoren)
Einige Befehle zum Umgang mit Polynomen haben wir schon im dritten Abschnitt kennengelernt. So koennen wir etwa zu
| > |
f:= x-> (x-1)*(x^3+x^2-1); |
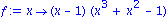
durch
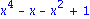
die uebliche ausmultiplizierte Darstellung des Ausdrucks bekommen. Nullstellen lassen sich mit dem Befehl
solve
ermitteln.

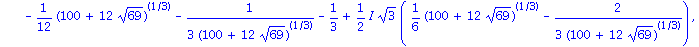
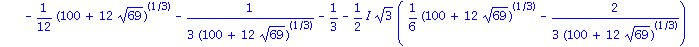
Als Gleitkommazahlen sehen die vier Nullstellen uebersichtlicher aus. Beachten Sie, dass hier wieder zwei komplexe Nullstellen auftauchen.
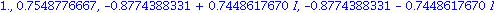
Veranschaulichung
Vielfaeltige graphischen Moeglichkeiten bilden einen wesentlichen Bestandteil von CAS Systemen wie Maple. Mit dem
plot
Befehl lassen sich Funktionen/Ausdruecke veranschaulichen.
Wir beginnen mit dem Graphen einer Funktion
f: R -> R,
wie er aus der Schule bekannt sein sollte. Das erste Argument muss eine Funktion oder einen Ausdruck enthalten. Das zweite Argument gibt den Definitionsbereich an.
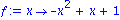
![[Plot]](images/kapitel-04maple_16.gif)
Wenn das erste Argument ein Ausdruck ist, muss beim Definitionsbereich die Variable angegeben werden. Weitere Argumente, zum Beispiel um den Wertebereich einzuschraenken, sind moeglich.
| > |
plot(f(x),x=-2..3,y=0..1,color=blue); |
![[Plot]](images/kapitel-04maple_17.gif)
Mit einer Vielzahl von Optionen (wie hier
color
) laesst sich der Plot nach eigenen Wuenschen gestalten.
Wollen wir mehrere Graphen (incl verschiedener Optionen) in einem Bild sehen, so bietet das Paket
plots
den Befehl
display
. Zum Beispiel die Umkehrfunktion zu f.
| > |
g:=x->sqrt(5/4-x) + 1/2; w:=x->x; |
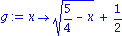
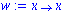
| > |
with(plots):
p1:=plot(f,1/2..2,color=blue,thickness=2):
p2:=plot(g,-1..5/4,color=red,thickness=2):
p3:=plot(w,-1..2,color=black,linestyle=4,thickness=2):
display(p1,p2,p3,scaling=constrained); |
Warning, the name changecoords has been redefined
![[Plot]](images/kapitel-04maple_20.gif)
Bem.: Pakete sind Sammlungen von Befehlen zu einem Thema, die aus Effizienzgruenden nur zur Verfuegung stehen, wenn sie mit dem Befehl
with
dazugeladen werden. Einzelne Befehle aus einem Paket lassen sich auch durch die Befehlsform wie plots[display] aufrufen. Eine Liste der Befehle, die in einem Paket zusaetzlich bereitgestellt werden, bekommen wir, wenn wir den Befehl durch ein Semikolon abschliessen.

Wir koennen Funktionen auch abschnittweise definieren. Dazu dient der Befehl
piecewise
. Als Beispiel sei etwa
| > |
f:=x->piecewise(x>=0, x^2,x<0,-x+a); |
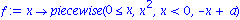
angegeben. Wenn wir den Graphen dieser Funktion betrachten wollen, so muessen wir dem System sagen, dass die Funktion unstetig sein kann, indem wir die Option discont = true im plot-Befehl verwenden,
| > |
a:= 2:
plot(f,-2..2,discont = true); |
![[Plot]](images/kapitel-04maple_27.gif)
oder die stetige Variante mit  :
:
| > |
a:= 0:
plot(f,-2..2,discont = true); |
![[Plot]](images/kapitel-04maple_29.gif)
Aufgaben
(Um Aufgaben zu bearbeiten oeffnen Sie bitte ein neues Worksheet und probieren Sie dort ihre Befehle aus. Einen Loesungsvorschlag erhalten Sie, wenn sie die Loesung oeffnen. Dies sollten Sie aber erst nach eigenen Versuchen nutzen.)
1. Gegeben sei die Funktion mit

Bestimmen Sie den Definitionsbereich dieser Funktion, ihre Nullstellen und erstellen Sie ein Bild des zugehoerigen Graphen.
Loesung
2. Zeigen Sie anschaulich durch ein Bild beider Graphen, dass die beiden Funktionen mit
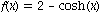 und
und 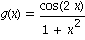
genau zwei Schnittpunkte haben, d.h. Stellen x auf der reellen Achse mit f(x)=g(x).
Loesung
3. In Aufgabe 4.11 soll die Umkehrfunktion zum Tangens-Hyperbolikus nachgerechnet werden. Verifizieren Sie mit Maple die Identitaeten
artanh( 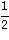
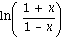 ) =
) = 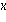
fuer 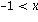 < 1, und
< 1, und
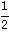
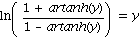
fuer 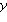 reell.
reell.
Loesung
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Plot]](images/kapitel-04maple_16.gif)
![[Plot]](images/kapitel-04maple_17.gif)
![[Plot]](images/kapitel-04maple_20.gif)
![[Plot]](images/kapitel-04maple_27.gif)
![[Plot]](images/kapitel-04maple_29.gif)