kapitel-13maple.mw
Mathematik
von T. Arens, F. Hettlich, Ch. Karpfinger, U. Kockelkorn, K. Lichtenegger, H. Stachel
(zu Kapitel 13: Differenzialgleichungen)
Der Befehl dsolve
Gewoehnliche Differenzialgleichungen,
F(  ,
,  ,...,
,...,  ,
,  ) = 0,
) = 0,
koennen direkt in der Maple-Syntax eingeben werden. So laesst sich z.B. die DGL
( )
)  '(
'( ) +
) + 

durch den Befehl
| > |
dgl:= (x^2+1)*D(y)(x) + 2*x*y(x) = 0; |
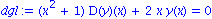
angeben. Eine Vielzahl von Techniken zur analytischen Loesung einer DGL steht nun mit dem entscheidenden Befehl
dsolve
zur Verfuegung.
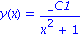
Da wir keinen Anfangswert zu der DGL erster Ordnung festgelegt haben, wird die allgemeine Loesung mit einer Konstante " " angeben. Eine Anfangsbedingung kann aber auch beruecksichtigt werden.
" angeben. Eine Anfangsbedingung kann aber auch beruecksichtigt werden.
| > |
abed:= y(0) = 2; lsg:=dsolve({dgl,abed},y(x)); |
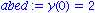
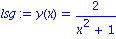
Beachten Sie die Syntax. Die DGL zusammen mit einer moeglichen Anfangsbedingung ist das erste Argument in Form einer Menge. Bei dieser Variante ist es notwendig, auch das zweite Argument, die gesuchte Funktion, mit anzugeben.
Das Resultat von dsolve ist ein Ausdruck und kann mit den allgemeinen Befehlen weiter bearbeitet werden. Zum Beispiel koennen wir uns den Graphen der Loesung ansehen.
![[Plot]](images/kapitel-13maple_15.gif)
(
rhs
liefert uns dabei die rechte Seite der Gleichung in dem Ausdruck  .)
.)
Auch einige Differentialgleichungen hoeherer Ordnung (s.u.) koennen von Maple geloest werden. Ausserdem sind eine ganze Reihe von Optionen zum dsolve Befehl moeglich. Zum Beispiel koennen wir die Potenzreihenmethode erzwingen und uns die zugehoerige formale Potenzreihe ausgeben lassen.
| > |
dgl2:= (D@@2)(y)(x) - (x+1)*y(x) = 0; |
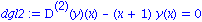
| > |
dsolve(dgl2,y(x),type='series'); |
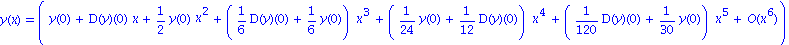
Das Paket DEtools
Mit dsolve haben wir schon den wichtigsten Befehl kennengelernt. Eine Vielzahl spezieller Befehle zur Behandlung von Differentialgleichungen, Differentialgleichungssytemen und partiellen Differentialgleichungen ist im Programmpaket
DEtools
zusammengestellt.
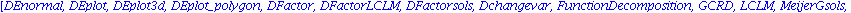
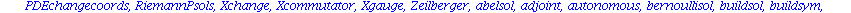
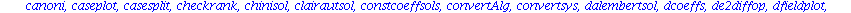
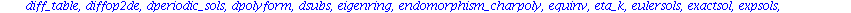
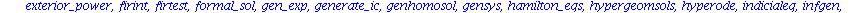
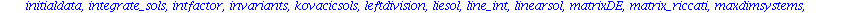
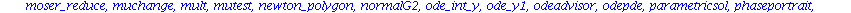
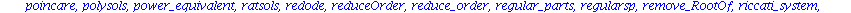
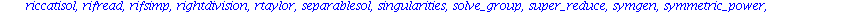
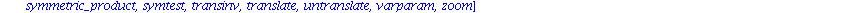
Wir koennen natuerlich nur einen kleinen Teil der aufgelisteten Befehle ansprechen und muessen fuer alles weitere auf die Hilfen oder die Literatur verweisen.
Beim Befehl dsolve wird der DGL zunaechst ein Typ zugeordnet, der ueber die anzuwendende Loesungsstrategie entscheidet. Diese Zuordnung erhalten wir mit dem Befehl
odeadvisor
.
![[_separable]](images/kapitel-13maple_29.gif)
Wenn Sie sich die Hilfedatei dazu ansehen, bekommen Sie einen guten Eindruck von den vielen Moeglichkeiten, die Maple bereitstellt. Ein weiterer nuetzlicher Befehl ist
odetest
, mit dem verifiziert werden kann, ob ein Ausdruck eine DGL loest.
| > |
odetest(y(x)=4/(1+x^2),dgl);
odetest(y(x)=x^2,dgl); |

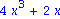
Im ersten Fall erhalten wir die Ausgabe 0, d.h. die DGL ist erfuellt. Im zweiten Fall hingegen erhalten wir den von Null verschiedenen Rest nach Einsetzen in die DGL. Selbstverstaendlich laesst sich eine vermeintliche Loesung auch mit dem Befehl
subs
testen.
| > |
f:=x->4/(1+x^2);
subs(y=f,dgl);
simplify(%); |
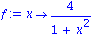
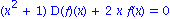

Mit odetest lassen sich auch bequem implizit gegebene Loesungen und Loesungen zu Differenzialgleichungssystemen ueberpruefen. Im folgenden wird auf das Verifizieren von Loesungen, die durch solve oder dsolve bestimmt wurden, verzichtet. Im allgemeinen sind solche Tests aber angebracht - Fehler verstecken sich gerne!
Sehr nuetzlich ist auch der Befehl
DEplot
, der zu einer gewoehnliche Differentialgleichungen erster Ordnung in der Form
y'(x) = f( x, y(x))
das Richtungsfeld zeichnet. Es wird also in jedem Punkt (x,y) der Ebene die Steigung 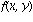 angetragen, die eine Loesung der Differentialgleichung an dieser Stelle haben muss. Zum Beispiel folgende Differentialgleichung:
angetragen, die eine Loesung der Differentialgleichung an dieser Stelle haben muss. Zum Beispiel folgende Differentialgleichung:
| > |
f:=(x,y)->y^2-2*x*y;
dgl:=D(y)(x)=f(x,y(x)); DEplot(dgl,y(x),x=-1..1,{[-1,0.2]},y=-0.5..1.5,linecolor=blue); |
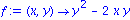
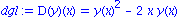
![[Plot]](images/kapitel-13maple_38.gif)
Das Verhalten einer konkreten Loesung ist aus den Richtungspfeilen zu erahnen. Die blaue Kurve zeigt die spezielle Loesung mit dem Anfangswert y(-1) = 0.2 . Beachten Sie die Syntax dieses Befehls, die leider verschieden ist vom dsolve Befehl. Die Gruende dafuer liegen in weiteren Moeglichkeiten des DEplot Befehls im Fall von DGL hoeherer Ordnung oder Systemen von DGL, auf die hier nicht eingegangen werden kann.
Nebenbei sei angemerkt, dass Sie die Ausgabe der Bilder auch auf eine Datei umlenken koennen. Entweder nutzen Sie das Popup-Menue, dass Sie bekommen, wenn Sie das Bild mit der rechten Maustaste anklicken, oder Sie nutzen den Befehl
plotsetup
. Wir koennen zum Beispiel eine Postscript Datei des Richtungsfeldes folgendermassen erzeugen.
(Achtung: Wenn Sie diesen Befehl ausfuehren, wird eine Datei mit dem Namen rfeld.ps erstellt bzw. ueberschrieben!)
| > |
plotsetup(cps,plotoptions=`color`,plotoutput=`rfeld.ps`);
DEplot(dgl,y(x),x=-1..1,{[-1,0.2]},y=-0.5..1.5,linecolor=blue); |
Mit
setzen wir die Eigenschaften des plot Befehls wieder zurueck.
Numerische Verfahren
Beim Befehl DEplot werden Loesungen zu Anfangswertproblemen numerisch approximiert. Es gibt eine Vielzahl von Verfahren, aber das einfachste ist sicherlich das im Buch besprochene Euler-Verfahren. Wir schreiben ein kurzes Programm, dass dieses Verfahren ausfuehrt.
| > |
myeuler:= proc(f,x0,y0,xN,h)
local x,y,yN,seq:
global eulerlist:
y:=y0:
seq:=NULL:
for x from x0 by h to xN do
yN := y:
seq := seq, [x,y]:
y := evalf(y+h*f(x,y)):
od:
eulerlist := [seq]:
yN;
end: |
Die Eingabevariablen sind
f - die Funktion f in zwei Variablen
x0 - die Anfangsstelle
y0 - der Anfangswert
xN - der Endpunkt
h - die Schrittweite
Darueberhinaus werden noch lokale Variable, x, y, yN, seq und eine globale Varaible eulerlist, die nach Ablauf des Programs eine Liste aller Approximationen enthaelt, definiert.
Nun kann das Verfahren ausgetestet werden. Betrachten wir wieder folgende DGL:
| > |
f:=(x,y)->y^2-2*x*y;
dgl:= D(y)(x) = f(x,y(x)); |
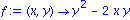
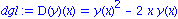
Eine Approximation der Loesung an der Stelle x=1 zum Anfangswert y(0)=1 erhalten wir durch
| > |
myeuler(f,-1,0.2,1,0.5); |
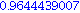
Wir halten das Ergebnis fest und verkleinern den Abstand der Stuetzstellen:
| > |
euler1:=plot(eulerlist,color=blue):
myeuler(f,-1,0.2,1,0.25); |
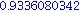
Wir nehmen noch eine Approximation mit h=1/100 hinzu und vergleichen die Ergebnisse.
| > |
euler2:=plot(eulerlist,color=red):
myeuler(f,-1,0.2,1,0.01); euler3:=plot(eulerlist,color=green):
with(plots): display([euler1,euler2,euler3]); |
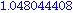
Warning, the name changecoords has been redefined
![[Plot]](images/kapitel-13maple_44.gif)
Selbstverstaendlich gibt es bessere numerische Verfahren als das Euler-Verfahren. Eine der gaengigsten Methoden, das Runge-Kutta-Verfahren, basiert auf einer geschickten Modifikation der hier aufgezeigten Idee und ist in Maple implementiert als Option zum dsolve-Befehl.
| > |
rk:=dsolve({dgl,y(-1)=0.2},y(x),numeric); |
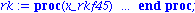
Maple erstellt eine Prozedur, die die approximierte Loesungsfunktion beinhaltet. Wir erhalten den Funktionswert an der Stelle x=1 durch
![[x = 1., y(x) = 1.06400664449019411]](images/kapitel-13maple_46.gif)
Einen plot dieser Loesung koennen wir uns mit dem Befehl
odeplot
aus dem DEtools Paket ansehen.
| > |
odeplot(rk,[x,y(x)],-1..1); |
![[Plot]](images/kapitel-13maple_47.gif)
Der Stossdaempfer
Nun wollen wir Maple fuer ein Anwendungsproblem nutzen - das Modell eines Stossdaempfers.
Die Auslenkung einer Masse m an einer Feder aus ihrer Ruhelage, L, sei durch y(t) bezeichnet. Nach dem zweiten Newtonschen Gesetz gilt, dass das Produkt aus Masse und Beschleunigung die Kraft ist,
m y''(t) = F( t, y(t), y'(t)).
Dabei setzt sich die Kraft aus mehreren Anteilen zusammen, F=F1+F2+F3+F4 mit
Gravitation: F1 = m g (g Erdbeschleunigung)
Rueckstellkraft: F2 = -k (y(t)+L) (k>0 Federkonstante)
Daempfung: F3 = -b y'(t) (b>0 Daempfungskonstante)
Externe Kraefte: F4 = f(t).
Da sich die Gravitation, F1, und die Rueckstellkraft in Ruhelage, F2 = -kL, ausgleichen, erhalten wir die lineare inhomogene DGL zweiter Ordnung (mit konstanten Koeffizienten)
m y''(t) + by'(t) +ky(t) = f(t)
Wir wollen das Verhalten einer solchen Feder unter verschiedenen Bedingungen analysieren.
Zunaechst raeumen wir auf, laden die noetigen Toolboxen und definieren die DGL
| > |
restart: with(plots): with(DEtools):
dgl:= (D@@2)(y)(t) + b/m*D(y)(t) + k/m*y(t) = f(t)/m; |
Warning, the name changecoords has been redefined
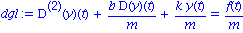
(a) Die ungedaempfte (b=0), freie (f=0), Schwingung:
| > |
f:=t->0; dgl1:=subs(b=0,dgl); dsolve(dgl1); |
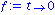
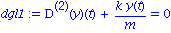
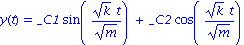
Wie zu erwarten ergibt sich eine harmonische Schwingung mit Frequenz  . Mit Festlegung einer Anfangsauslenkung und einer Anfangsgeschwindigkeit erhalten wir die eindeutig bestimmte Loesung, zum Beispiel
. Mit Festlegung einer Anfangsauslenkung und einer Anfangsgeschwindigkeit erhalten wir die eindeutig bestimmte Loesung, zum Beispiel
| > |
abed:= y(0)=0, D(y)(0)=-1; dsolve({dgl1,abed},y(t)); |
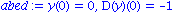
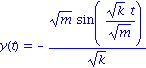
(b) Die gedaempfte, freie Schwingung:
Im folgenden legen wir m=1 und k=1 fest und betrachten eine Daempfungskonstante  .
.
| > |
dgl2:=subs(b=1/10, m=1, k=1, dgl); |
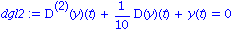
| > |
lsg:=rhs(dsolve({dgl2,abed},y(t))); |
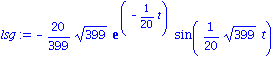
![[Plot]](images/kapitel-13maple_58.gif)
Erhoehen wir die Daempfung der Feder so erreichen wir bei b=2 einen kritischen Bereich.
| > |
dgl3:=subs(b=1, m=1, k=1, dgl);
lsg:=rhs(dsolve({dgl3,abed},y(t))); plot(lsg,t=0..10*Pi); |
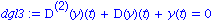
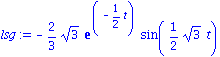
![[Plot]](images/kapitel-13maple_61.gif)
Wir aendern die Anfangsbedingung, um den Effekt deutlicher zu sehen:
| > |
abed:= y(0)=0.5, D(y)(0)=-1;
dgl3:=subs(b=2, m=1, k=1, dgl);
lsg:=rhs(dsolve({dgl3,abed},y(t))); plot(lsg,t=0..10*Pi); |
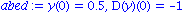
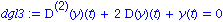
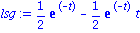
![[Plot]](images/kapitel-13maple_65.gif)
Die Feder schwingt einmal durch und kommt wieder in die Ruhelage zurueck. Eine weitere Erhoehung der Daempfung fuehrt in den uebergedaempften Bereich wie bei einem intakten Stossdaempfer.
| > |
dgl4:=subs(b=3, m=1, k=1, dgl);
lsg:=rhs(dsolve({dgl4,abed},y(t))); plot(lsg,t=0..10*Pi); |
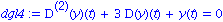
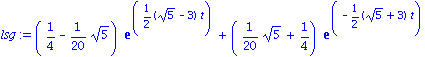
![[Plot]](images/kapitel-13maple_68.gif)
(c) Erzwungene Schwingungen:
Es sei angenommen, dass eine zusaetzliche Kraft auf die Feder wirkt, zum Beispiel
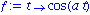
Mit einer Frequenz  erhalten wir folgende Loesung
erhalten wir folgende Loesung
| > |
dgl4:=subs(a=1/2, b=1/10, m=1, k=1, dgl);
abed:= y(0)=0, D(y)(0)=-1; |
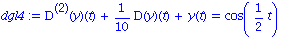
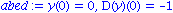
| > |
lsg4:=dsolve({dgl4,abed},y(t)): lsg4:=collect(lsg4,exp); |
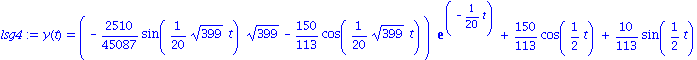
Uff! - mit dem Befehl
collect
ist uebrigens der exponentielle Anteil ausgeklammert worden. Der stationaere Teil der Loesung (also ohne den exponentiellen Anteil) laesst sich mit dem Befehl
remove
aus diesem Ausdruck extrahieren.
| > |
st_lsg4:= remove(has,rhs(lsg4),exp(-1/20*t)); |
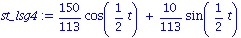
Nun lassen sich die Graphen der beiden Schwingungen vergleichen
| > |
pe:=plot(rhs(lsg4), t=0..30*Pi, color=red):
ps:=plot(st_lsg4, t=0..30*Pi, color=blue):
display([pe,ps]); |
![[Plot]](images/kapitel-13maple_75.gif)
Nach einer gewissen Zeit verhaelt sich also die erzwungene Schwingung wie die stationaere Loesung.
Das Verhalten von Loesungen in Hinblick auf die Frequenz a der anregenden aeusseren Kraft soll nun noch genauer untersucht werden.
| > |
dgl5:=subs(m=1, k=1, dgl); |
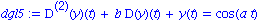
Wir ermitteln eine Resonanzfrequenz aus den Nullstellen des charakteristischen Poynoms.
| > |
lambda := solve(x^2+b*x+1=0,x): l1:=lambda[1]; assume(b>0,b<2): a:=Im(l1); |
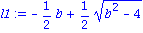
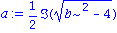
Mit einer Daempfungskonstante b=0.1 erhalten wir die Loesung
| > |
dgl6:=subs(b=1/10,m=1, k=1, dgl); |
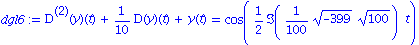
| > |
lsg:=rhs(dsolve({dgl6,abed},y(t))): plot(lsg,t=0..50*Pi); |
![[Plot]](images/kapitel-13maple_80.gif)
Beachten Sie, die Hoehe der Amplituden, die um ein 10faches groesser sind als die anregende Schwingung.
Ohne Daempfung ist die Situation noch kritischer, da die Amplituden mit der Zeit linear anwachsen.
| > |
dgl7:=subs(b=0,m=1, k=1, dgl); |
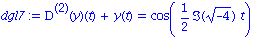
| > |
lsg:=rhs(dsolve({dgl7,abed},y(t))): plot(lsg,t=0..30*Pi); |
![[Plot]](images/kapitel-13maple_82.gif)
Aufgaben
(Um Aufgaben zu bearbeiten oeffnen Sie bitte ein neues Worksheet und probieren Sie dort ihre Befehle aus. Einen Loesungsvorschlag erhalten Sie, wenn sie die Loesung oeffnen. Dies sollten Sie aber erst nach eigenen Versuchen nutzen.)
1. Bestimmen Sie die Loesungen zu folgenden Anfangswertproblemen. Betrachten Sie die Graphen dieser Funktionen und diskutieren Sie, welches Verhalten der Loesung Sie schon direkt aus der DGL erwarten konnten.
a) 
 '(
'( ) + (
) + ( )
)  (
( ) = 0,
) = 0, 
b)  (
( )
)  '(
'( ) =
) =  ,
, 
Loesung
2. Diskutieren Sie anhand des Richtungsfeldes das Verhalten von Loesungen der DGL
y'(x) = x+sin(y(x))
und erstellen Sie mit DEplot eine Ausgabe, die die Loesungen zu den Anfangsbedingungen
y(0)=-1, y(0)=0 und y(0)=1
ohne das Richtungsfeld zeigt.
Loesung
3. Loesen Sie die Differentialgleichungen
a) y''(x) + (1-I) y'(x) - I y(x) = 0,
b) y'''(x) - 3y''(x) + 4y(x) = 0,
c) y^(5)(x) - y(x) = 0
und die Anfangswertprobleme
d) u''''(x) - u'''(x)-u''(x)-u'(x) - 2*u(x) = 0 mit u(0) = 0, u'(0) = 0, u''(0) = 0, u'''(0) = 1
e) x^2*y''(x) - 2*x*y'(x) + 2*y(x) = 0 mit y(1) = 0, y'(1) = -1 .
Loesung
![]() ,
, ![]() ,...,
,..., ![]() ,
, ![]() ) = 0,
) = 0,![]() )
) ![]() '(
'(![]() ) +
) + ![]()
![]()
![]()
![]()
![]() " angeben. Eine Anfangsbedingung kann aber auch beruecksichtigt werden.
" angeben. Eine Anfangsbedingung kann aber auch beruecksichtigt werden.![]()
![]()
![[Plot]](images/kapitel-13maple_15.gif)
![]() .)
.)![]()
![]()
![[Plot]](images/kapitel-13maple_38.gif)
![[Plot]](images/kapitel-13maple_44.gif)
![[Plot]](images/kapitel-13maple_47.gif)
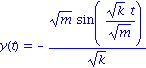
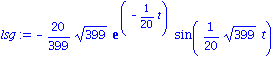
![[Plot]](images/kapitel-13maple_58.gif)
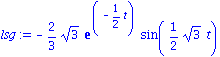
![[Plot]](images/kapitel-13maple_61.gif)
![[Plot]](images/kapitel-13maple_65.gif)
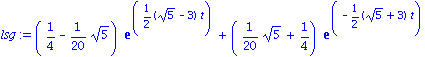
![[Plot]](images/kapitel-13maple_68.gif)
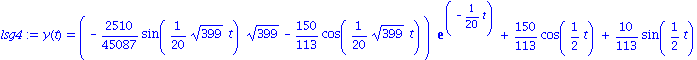
![[Plot]](images/kapitel-13maple_75.gif)
![[Plot]](images/kapitel-13maple_80.gif)
![[Plot]](images/kapitel-13maple_82.gif)